X = originX + radiusX * Cos(freqX * T) Y = originY + radiusY * Sin(freqY * T) |
 The formula for an ellipse is listed above.
For now, we are only going to concern ourselves with the origin and radius. We will discuss the frequency later.
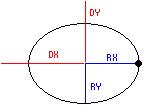
For the ellipse in the picture, you can see the two radii (radiuses ha ha ha) as RX and RY in blue, and these define how the ellipse is
shaped. If the two radii have the same value, then you have a circle.
Also, in the picture are two distances DX and DY in red, which specify the coordinates of the center of the ellipse. Changing these
will move the ellipse around.
So, use the formula: X = DX + RX * Cos(T) ; Y = DY + RY * Sin(T) and you'll get some sort of circle.
The formula for an ellipse is listed above.
For now, we are only going to concern ourselves with the origin and radius. We will discuss the frequency later.
For the ellipse in the picture, you can see the two radii (radiuses ha ha ha) as RX and RY in blue, and these define how the ellipse is
shaped. If the two radii have the same value, then you have a circle.
Also, in the picture are two distances DX and DY in red, which specify the coordinates of the center of the ellipse. Changing these
will move the ellipse around.
So, use the formula: X = DX + RX * Cos(T) ; Y = DY + RY * Sin(T) and you'll get some sort of circle.
A circle with a radius of 50 at 100,100. X = 100 + 50 * Cos(T) Y = 100 + 50 * Sin(T) Circle has both radii set to 50. |
An ellipse where the radius is 200 in the X and 40 in the Y. It will go around the point 450, 270. X = 450 + 200 * Cos(T) Y = 270 + 40 * Sin(T) |
I want my shape to go from (100, 150) to (400, 380). Find the middle point by averaging the two X points ((400 + 100)/2 = 250) and the two Y points ((380 + 150)/2 = 265). The center is at 250, 265. The radius in the X directions would be 400 - 250 = 150, while the radius in the Y directions would be 380 - 265 = 115. (Just subtract the point location from the origin location to get the radius). X = 250 + 150 * Cos(T) Y = 265 + 115 * Sin(T) |
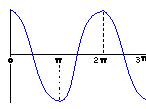 Cosine Wave and
Cosine Wave and 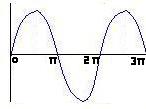 Sine Wave.
The parts after 2 * Pi continue on forever.
We can tamper with the period by multiplying T by a number.
For instance: Cos(2 * T) will cause cosine to reach 2 * Pi in half the time.
Cos(3 * T) will make cosine reach 2 * Pi in a third of the time.
So, multiplying the T by a mystery number causes the period to be divided by this mystery number.
Cos(2 * T) would now have a period of Pi. Cos(Pi * T) would have a period of 2. And, of course,
Cos(2 * Pi * T) would have a period a 1.
This multiplying number is what I call the angular frequency, and I usually just write Freq in programs.
This is not the actual frequency of our function. The original frequency of Cos(T) is 1 / (2*Pi).
The angular frequency is represented by multiplying the current frequency by the original period 2 * Pi
(or multiplying the current period by the original frequency)
But, in short, angular frequency is the number that multiplies by T (as I have just mentioned).
In Cos(T), the angular frequency is 1, and in Cos(3T), the angular frequency is 3.
Keeping the angular frequency at 1 might look simple, but if you put this into a program, the circle
will skip too many points for someone to notice it.
You'll need to decrease the angular frequency before the circle is traced decently. 0.1 is usually a
good value for the circle to be noticed, but smaller values will trace the circle out with more care (and with
more time).
Sine Wave.
The parts after 2 * Pi continue on forever.
We can tamper with the period by multiplying T by a number.
For instance: Cos(2 * T) will cause cosine to reach 2 * Pi in half the time.
Cos(3 * T) will make cosine reach 2 * Pi in a third of the time.
So, multiplying the T by a mystery number causes the period to be divided by this mystery number.
Cos(2 * T) would now have a period of Pi. Cos(Pi * T) would have a period of 2. And, of course,
Cos(2 * Pi * T) would have a period a 1.
This multiplying number is what I call the angular frequency, and I usually just write Freq in programs.
This is not the actual frequency of our function. The original frequency of Cos(T) is 1 / (2*Pi).
The angular frequency is represented by multiplying the current frequency by the original period 2 * Pi
(or multiplying the current period by the original frequency)
But, in short, angular frequency is the number that multiplies by T (as I have just mentioned).
In Cos(T), the angular frequency is 1, and in Cos(3T), the angular frequency is 3.
Keeping the angular frequency at 1 might look simple, but if you put this into a program, the circle
will skip too many points for someone to notice it.
You'll need to decrease the angular frequency before the circle is traced decently. 0.1 is usually a
good value for the circle to be noticed, but smaller values will trace the circle out with more care (and with
more time).
 Private Sub Timer1_Timer()
Dim X As Long, Y As Long
X = 100 + 50 * Cos(0.1 * T) 'Calculate circle point coordinates.
Y = 100 + 50 * Sin(0.1 * T)
'Set this pixel to white on my display.
SetPixel Me.hdc, fX, fY, vbWhite
T = T + 1
End Sub
Now, if you happen to set the two angular frequencies to different values, you'll get an assortment of different curvy shapes.
Doubling the X frequency:
X = 100 + 50 * Cos(0.2 * T)
Y = 100 + 50 * Sin(0.1 * T)
will give you a catenary curve (a parabola that doesn't extend to infinity).
Private Sub Timer1_Timer()
Dim X As Long, Y As Long
X = 100 + 50 * Cos(0.1 * T) 'Calculate circle point coordinates.
Y = 100 + 50 * Sin(0.1 * T)
'Set this pixel to white on my display.
SetPixel Me.hdc, fX, fY, vbWhite
T = T + 1
End Sub
Now, if you happen to set the two angular frequencies to different values, you'll get an assortment of different curvy shapes.
Doubling the X frequency:
X = 100 + 50 * Cos(0.2 * T)
Y = 100 + 50 * Sin(0.1 * T)
will give you a catenary curve (a parabola that doesn't extend to infinity).
 Doubling the Y frequency:
X = 100 + 50 * Cos(0.1 * T)
Y = 100 + 50 * Sin(0.2 * T)
will give you a figure-eight.
Doubling the Y frequency:
X = 100 + 50 * Cos(0.1 * T)
Y = 100 + 50 * Sin(0.2 * T)
will give you a figure-eight.
 Of course, changing the radii will cause the figure eight to take up a specific radius as well.
Experiment with these frequencies to get some more interesting shapes. You may have to decrease the
frequencies to see something clearer.
X = 100 + 50 * Cos(0.2 * T)
Y = 100 + 50 * Sin(0.15 * T)
Of course, changing the radii will cause the figure eight to take up a specific radius as well.
Experiment with these frequencies to get some more interesting shapes. You may have to decrease the
frequencies to see something clearer.
X = 100 + 50 * Cos(0.2 * T)
Y = 100 + 50 * Sin(0.15 * T)
