Periodics: Non-sinusoidal Periodics

Right now, we can make circles with our sinusoids, but what about other shapes, like stars, rectangles, and triangles?
To make shapes like this, we cannot use just Cos() and Sin().
One method might involve a large sum of Cos() and Sin() calls, but that is in the domain of Fourier, and that is not
where we are trying to go. 

The simpler method would be for us to make our own periodic functions.
It's much easier than it sounds.
Ideally, all of our made up periodic functions will be able to be used in the same way that we use Sin() and 
Cos().  We will have:
X = DX + RX * F(wX * T)
Y = DY + RY * F(wY * T)
I used wX and wY to denote angular frequency.


Also, all of our functions *should* remain in the range of [-1, 1], just like in Sin() and Cos().
However, we are under no obligation to make our function have a period of 2 * Pi.
I, personally, like to have my functions with a period of 1 so that the angular frequency is equal to the true
frequency.  
Now, let's get to making our periodic functions.

The easiest periodic function to make (at least I think so) would be the square wave.  It's also, unfortunately, the most useless.
The squarewave is just 1 from 0 to Pi, and -1 from Pi to 2 * Pi.

One simple demonstration of the Squarewave function would be something like this:

Public Function SquareWave(N As Single) As Single
SquareWave = Sgn(Sin(N))
'This will be (mostly) 1 for 0 to Pi and -1 for Pi to 2 * Pi.
End Function

And here's how we might test it.
Private Sub Timer1_Timer()
Dim fX As Long, fY As Long
fY = 100 + 50 * SquareWave(0.1 * T)  'Call squarewave.
SetPixel Me.hdc, T, fY, vbWhite
'Illustrates our function.
T = T + 1
End Sub


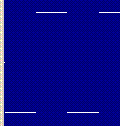There's our simple squarewave.  You can slap this in the periodic function library.
One small observation for really nitpickiness.  The signum function, a.k.a. Sgn() function will return 0 if
Sin() returns 0.  This means that SquareWave(0) will return 0.  Ideally, for SquareWave to only take on the values of 1
and -1, having it return 0 would be a violation.  Note that SquareWave would also return 0 for SquareWave(Pi).

We can fix this by properly setting up the function ourselves.
Pay attention: this is how we will be creating a gaggle of other periodic functions.

We will redefine the SquareWave function.
First we will take the input parameter (N As Single), and divide it by the period.
Note that if we make the actual period 1, then we won't have to divide and we save a division's worth of time in our
code execution.

Now, we need to actually get our results into this range, because we do not have those values defined.
So, we will have to do a modulus operation for floating point numbers.
This is not overly complicated, and is quite easy to do.
Res = (N / Period - Int(N / Period)) * Period
Note that N / Period should already have been calculated.
Int rounds a floating point number down to an integer.

I use
Public Function Fmd(Quotient As Single, Denom As Single) As Single
Fmd = (Quotient - Int(Quotient)) * Denom
'Quotient is Numerator / Denom(inator).
End Function
often in my periodic function calculations.
We cannot bypass this modulus operation, regardless of what our period is.  (Otherwise our function wouldn't be
periodic)

With this result, we use some if statements, so if our result is in [0 , halfperiod) we return 1, and if [halfperiod, period) we return -1.
If Res >= 0 And Res < 0.5 Then
  SquareWave = 1
Else
  SquareWave = -1
End If

Note again that if our period is 1, we only have to check 0 and 0.5, as I have done above.
Here are some other SquareWave implementations.
Public Function SquareWave2(N As Single) As Single
Dim Res As Single
Res = Fmd(N, 1)
If Res >= 0 And Res < 0.5 Then
  SquareWave2 = 1
Else
  SquareWave2 = -1
End If
End Function

This is the aforementioned SquareWave with period of 1.
Public Function SquareWave3(N As Single) As Single
Const Period As Single = 2
Dim Quotient As Single, Res As Single
Quotient = N / Period
Res = Fmd(Quotient, Period)
If Res >= 0 And Res < Period / 2 Then
  SquareWave3 = 1
Else
  SquareWave3 = -1
End If
End Function

This is a version where you can set the value of period to whatever you want.


And that's our SquareWave function.

Applying the SquareWave function to the periodic form equations at the very top of this page:
X = 100 + 25 * SquareWave2(0.5 * T)
Y = 100 + 25 * SquareWave2(0.4 * T)

We eventually max out with 4 dots.

If the squarewaves are set to the same angular frequency, you'll only get two dots.

Now, enough with this, how do we make a square!
Well, that's what we are going to discuss next, the Triangle Wave.
It sounds quite odd that we are going to make a square with a TriangleWave, but that's just how it is.

This is what the TriangleWave is supposed to look like:


Now, how to make it.
Well, we'll keep all of the original 'initialization' stuff from SquareWave:
Const Period As Single = 2
Dim Quotient As Single, Res As Single
Quotient = N / Period
Res = Fmd(Quotient, Period)

Now, we examine Res.  Since the period is two, we want the TriangleWave to be going down along the line when Res is from 
[ 0 , 1 ), and going up when Res is from [ 1 , 2 ).
This will require us to write some line equations in each portion of the If statement.
(First off, we are just going to assume the period will be 2 to simplify the calculation).

For the first part If Res >= 0 And Res < 1 Then
we have a line that has a slope of -2 -- rise/run = (-1 - +1) / (+1 - +0) = -2.  The Y-intercept is 1, so our line equation
would be:
Trgl = -2 * Res + 1
The second line has a slope of 2.  I will shortcut by saying that the intercept is -1 by using (Res - 1) instead of just Res.
So, our second equation would be:
Trgl = 2 * (Res - 1) - 1.
Without using (Res - 1), you'd get the Y-intercept to be -3 and the equation to be 2 * Res - 3.
You can orient the triangle either up or down.  It usually gets foggy because of computer coordinates draw higher values to
the bottom and smaller values to the top.

So, now we have our TriangleWave function:
Public Function Trgl(N As Single) As Single
Dim Quotient As Single, Res As Single
Quotient = N / 2
Res = Fmd(Quotient, 2)
If Res >= 0 And Res < 1 Then
  Trgl = 1 - 2 * Res  'Leading edge of triangle.
Else
  Trgl = 2 * (Res - 1) - 1   'Trailing edge of triangle.
End If
End Function

Now, how do we turn this into a square?

Like this:
X = 100 + 40 * Trgl(0.04 * T)
Y = 100 + 40 * Trgl(0.04 * T + 0.5)

I suppose I have to explain the 0.5.
The 0.5 is called the phase shift, but it starts the periodic function at a different location.
When T = 0, the first call to our lower Trgl will see 0.5.  This will cause Trgl to return 0 (the middle of the
leading edge of our TriangleWave.  This gives us the points on our square. 


And remember, a "diamond" is merely a square (or in a more general term, a rhombus) rotated 45 degrees.
This is how we would draw a square (diamond).

How would we draw a square?
OK, beat it on out of me.  This time we are going to make a run-of-the-mill, everybody-calls-it-the-same, garden-variety
square.

We have to use a HexagonWave.  The HexagonWave is quite difficult in that it consists of four regions, as shown in the
picture.
  (Do flip the picture over in your mind... the first edge is supposed to go up).
This means that instead of two sections within the If, we have four, and we will have to divide the period by 4 to get each
different zone.
Right now, we'll just set the period to be 4 to simplify the calculations, again.
Everything above Res = Fmd() will be the same, however (just change the period).  So, 
all we need to be concerned about is the bottom.
The first part of the hexagon wave: If Res >= 0 And Res < 1 Then
Is a line that starts at -1 and goes up to 1, so the slope would be 2, and the intercept would be -1.
Hxgn = 2 * Res - 1
The second part of the hexagon wave: If Res >= 1 And Res < 2 Then
Is always 1 
The third part of the hexagon wave is line where the slope is -2 and the intercept is 1.
Hxgn = -2 * (Res - 2) + 1
The final part is always -1.
So, that's our function.
Public Function Hxgn(N As Single) As Single
Dim Quotient As Single, Res As Single
Quotient = N / 4
Res = Fmd(Quotient, 4)
If Res >= 0 And Res < 1 Then
  Hxgn = 2 * Res - 1                'Rising edge of hexagon wave.
ElseIf Res >= 1 And Res < 2 Then
  Hxgn = 1                          'Top part.
ElseIf Res >= 2 And Res < 3 Then
  Hxgn = -2 * (Res - 2) + 1         'Falling edge of hexagon wave.
Else
  Hxgn = -1                         'Bottom part.
End If
End Function

Now, how do we make the square?
Well, we'll need to phase shift one of our coordinates to the next part of the hexagon wave.

X = 100 + 40 * Hxgn(0.04 * T)
Y = 100 + 40 * Hxgn(0.04 * T + 1)