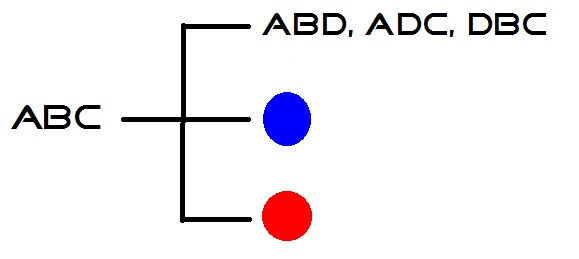
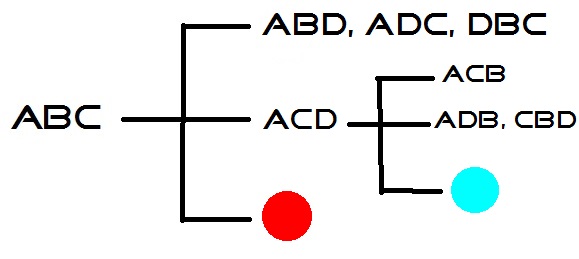
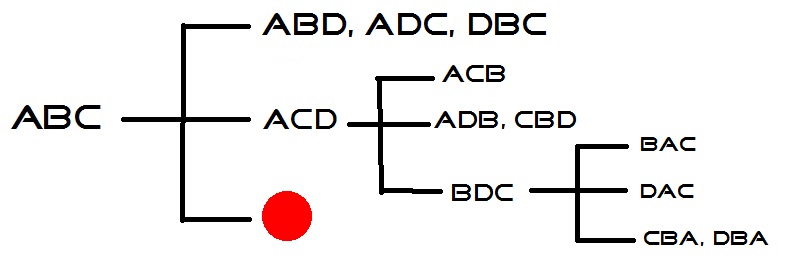
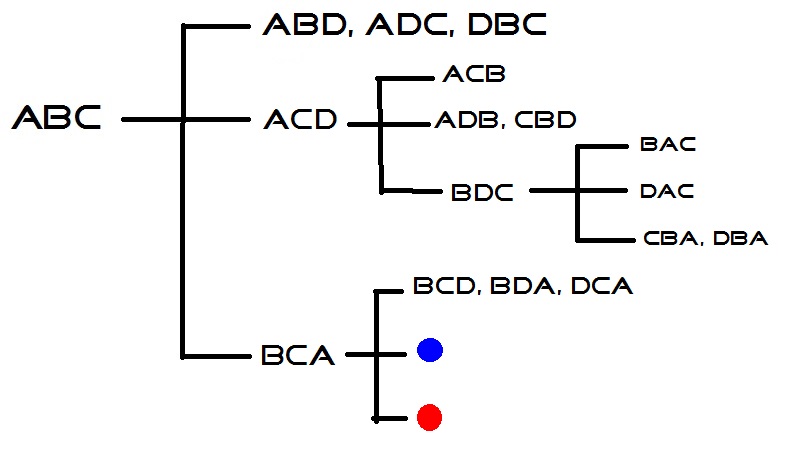
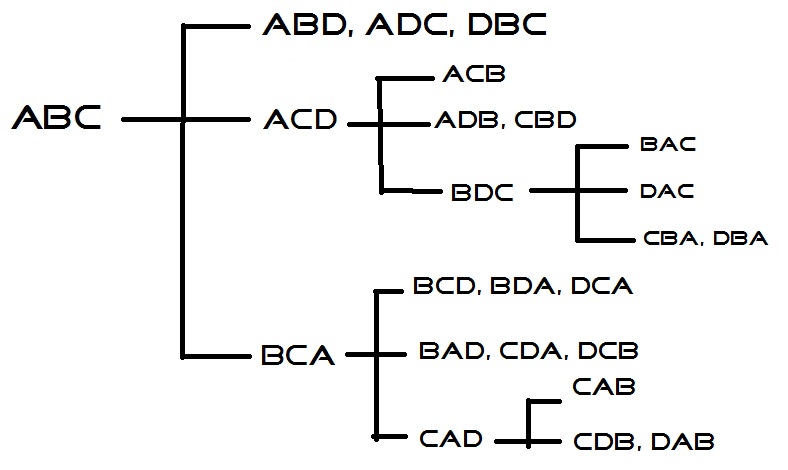
| 2 correct, possible answers: (3/23 entries) | ABD | ADC | DBC |
| 1 correct, possible answers: (9/23 entries) | ACB | ACD | ADB | BAC | BDC | CBA | CBD | DAC | DBA |
| 0 correct, possible answers: (11/23 entries) | BAD | BCA | BCD | BDA | CAB | CAD | CDA | CDB | DAB | DCA | DCB |
Notice the case where 2 are correct. In this case, the solution is either ABD, ADC, or DBC, and I can pick either one with a 1/3 chance of it being correct. However, if I don't pick the correct one, I will always get a result of '1 correct' (if DBC is the correct answer, ABD has '1 correct' with the B and ADC has '1 correct' with the C; the same applies to the other choices if either ABD or ADC is the right answer). So, in this case, I can pick at random among the three until I get the correct answer.