Note that having a periodic function is not solely limited to
Origin + Rad * F(AngFreq * T + offset)
We can do many operations to get different results. For example, we
can add two of these together. Then, we'll have something like this:
Origin1 + Origin2 + Rad1 * F1(AngFreq1 * T + offset1) + Rad2 * F2(AngFreq2 * T + offset2)
or
Origin + Rad1 * F1(AngFreq1 * T + offset1) + Rad2 * F2(AngFreq2 * T + offset2)
This new periodic function, depending on how the two
inner periodic functions (F1 and F2) behave with each
other, will have a radius of Rad1 + Rad2. (Of course,
the radii cannot be factored from this expression, so
you'll just have to go with it).
(These functions are similar to having the origin change by a periodic function)
For example, we can add two Sine functions together. Remeber that
this is a circle (radius of 40)
X = 50 + 40 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T)
but we can add another Sine function to this circle as well.
X = 50 + 40 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.4 * T)
So, now, in addition to the circle with radius of 40, we have a
little bit of fluctuation within the Y direction. You'll see that it
effectively makes a sinewave travel along the circle.
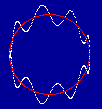 The red shows the circle without the 10 * Sin(0.4 * T)
The white shows the circle with the sine function added to it. As you
may be able to tell, the radius of this new figure is about 50
in the vertical direction.
Also, we can do
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.4 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.4 * T)
to get
The red shows the circle without the 10 * Sin(0.4 * T)
The white shows the circle with the sine function added to it. As you
may be able to tell, the radius of this new figure is about 50
in the vertical direction.
Also, we can do
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.4 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.4 * T)
to get
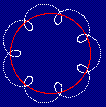 You may wonder why there are 7 loops? It does not have anything to do
with the 50 and 120 being 70 apart. The seven loops come from the
two different angular frequencies... the second angular frequency is
8 times the first angular frequency. That might not appear to explain the
seven loops, but it does if you consider the entire circle to be a loop as
well. After all, if you set the second frequency to be the same as the
first, then you get a plain circle (you can see by doing some algebra)
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.05 * T)
is equivalent to
X = 50 + 50 * Cos(0.05 * T)
Y = 120 + 50 * Sin(0.05 * T)
So, that would be one loop, and
You may wonder why there are 7 loops? It does not have anything to do
with the 50 and 120 being 70 apart. The seven loops come from the
two different angular frequencies... the second angular frequency is
8 times the first angular frequency. That might not appear to explain the
seven loops, but it does if you consider the entire circle to be a loop as
well. After all, if you set the second frequency to be the same as the
first, then you get a plain circle (you can see by doing some algebra)
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.05 * T)
is equivalent to
X = 50 + 50 * Cos(0.05 * T)
Y = 120 + 50 * Sin(0.05 * T)
So, that would be one loop, and
 has eight loops: seven on the inside, surrounded by one big loop.
We can add any kind of periodic functions together. The only
constraint that we have with doing periodics is that all of the
function calls with T have to be periodic. So, we can have
something like this
X = 50 + 20 * Cos(0.01 * T) + 10 * Cos(0.07 * T) + 20 * Hxgn(0.02 * T)
Y = 120 + 40 * Sin(0.01 * T) + 10 * Sin(0.07 * T) + 10 * Trpz(0.002 * T)
Of course it looks like scribble scratch because the periods of
Hxgn and Trpz don't match Sine and Cosine's period... eww.
has eight loops: seven on the inside, surrounded by one big loop.
We can add any kind of periodic functions together. The only
constraint that we have with doing periodics is that all of the
function calls with T have to be periodic. So, we can have
something like this
X = 50 + 20 * Cos(0.01 * T) + 10 * Cos(0.07 * T) + 20 * Hxgn(0.02 * T)
Y = 120 + 40 * Sin(0.01 * T) + 10 * Sin(0.07 * T) + 10 * Trpz(0.002 * T)
Of course it looks like scribble scratch because the periods of
Hxgn and Trpz don't match Sine and Cosine's period... eww.
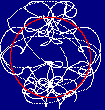 A nicer pic can be made by taking functions with similar periods and using
angular frequencies that have common factors.
For example:
X = 80 + 40 * Hxgn(0.01 * T) + 10 * Scln(0.05 * T) + 10 * Trpz(0.05 * T)
Y = 120 + 40 * Hxgn(0.01 * T + 1) + 15 * Scln(0.05 * T + 1)
A nicer pic can be made by taking functions with similar periods and using
angular frequencies that have common factors.
For example:
X = 80 + 40 * Hxgn(0.01 * T) + 10 * Scln(0.05 * T) + 10 * Trpz(0.05 * T)
Y = 120 + 40 * Hxgn(0.01 * T + 1) + 15 * Scln(0.05 * T + 1)
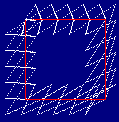 It looks a little horrendous at the start, but you can see that it
comes to a nice closure within three loops.
Note that in addition to addition (oops, no pun intended), we can combine
two periodic functions with multiplication.
(The radius changes according to a periodic function)
We'll have something like
Origin + Radius1 * Radius2 * F1(AngFreq * T + offset) * F2(AngFreq * T + offset)
The product of the two periodic functions will also be periodic, going
from -1 to 1.
So, we can have something like this:
X = 80 + 40 * Sin(0.02 * T) * Cos(0.06 * T)
Y = 120 + 40 * Cos(0.02 * T) * Cos(0.06 * T)
It looks a little horrendous at the start, but you can see that it
comes to a nice closure within three loops.
Note that in addition to addition (oops, no pun intended), we can combine
two periodic functions with multiplication.
(The radius changes according to a periodic function)
We'll have something like
Origin + Radius1 * Radius2 * F1(AngFreq * T + offset) * F2(AngFreq * T + offset)
The product of the two periodic functions will also be periodic, going
from -1 to 1.
So, we can have something like this:
X = 80 + 40 * Sin(0.02 * T) * Cos(0.06 * T)
Y = 120 + 40 * Cos(0.02 * T) * Cos(0.06 * T)
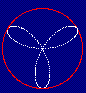 You can clearly see the 3 prongs of the fan are due to 0.06 being 3 times 0.02.
What you may not see is that changing the second pair of angular frequencies to
8 gives you eight fan blades, instead of 4 that you might expect.
This is because at the halfway point, Cos(0.02 * T) is halfway finished with the
circle and is -1, Cos(0.06 * T) is also halfway at -1. These two -1s multiply
together to give a +1, which means that at the halfway point, the periodic function
completes a lap. At the halfway point of Cos(0.02 * T), Cos(0.08 * T) has
already returned to the beginning, so it is at 1, and these multiply together to
give -1, so the drawing has not completed yet.
Of course, you can multiply more together to get something like
You can clearly see the 3 prongs of the fan are due to 0.06 being 3 times 0.02.
What you may not see is that changing the second pair of angular frequencies to
8 gives you eight fan blades, instead of 4 that you might expect.
This is because at the halfway point, Cos(0.02 * T) is halfway finished with the
circle and is -1, Cos(0.06 * T) is also halfway at -1. These two -1s multiply
together to give a +1, which means that at the halfway point, the periodic function
completes a lap. At the halfway point of Cos(0.02 * T), Cos(0.08 * T) has
already returned to the beginning, so it is at 1, and these multiply together to
give -1, so the drawing has not completed yet.
Of course, you can multiply more together to get something like
 fX = 80 + 40 * Sin(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
fY = 120 + 40 * Cos(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
Where the six big prongs come from the 0.06 and the 0.02, and the four smaller
prongs combining to make 10 prongs in total come from 0.1 and 0.02.
Remember that the only constraint is that T must be in a periodic function.
So, we have had periodic addition where "the origin change by a periodic function", and
we had periodic multiplication where "the radius changes by a periodic function".
Of course, we can make the final two parameters change by periodic functions... namely the
angular frequency and the offset.
With the angular frequency modified, we'll have something like this:
Origin + Radius * F1(AngFreq1 * F2(AngFreq2 * T + offset2) + offset1)
(The radius and angfreq multiplied to give the AngFreq1.
AngFreq1 has to be suitably large, otherwise the function might appear to be stuck
at a certain value.
X = 80 + 40 * Sin(1 * Sin(0.02 * T))
Y = 120 + 40 * Cos(1 * Sin(0.02 * T))
fX = 80 + 40 * Sin(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
fY = 120 + 40 * Cos(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
Where the six big prongs come from the 0.06 and the 0.02, and the four smaller
prongs combining to make 10 prongs in total come from 0.1 and 0.02.
Remember that the only constraint is that T must be in a periodic function.
So, we have had periodic addition where "the origin change by a periodic function", and
we had periodic multiplication where "the radius changes by a periodic function".
Of course, we can make the final two parameters change by periodic functions... namely the
angular frequency and the offset.
With the angular frequency modified, we'll have something like this:
Origin + Radius * F1(AngFreq1 * F2(AngFreq2 * T + offset2) + offset1)
(The radius and angfreq multiplied to give the AngFreq1.
AngFreq1 has to be suitably large, otherwise the function might appear to be stuck
at a certain value.
X = 80 + 40 * Sin(1 * Sin(0.02 * T))
Y = 120 + 40 * Cos(1 * Sin(0.02 * T))
 The red circle does not have the same radius as the white circle in the picture or
in the following pictures.
You can see that this function never quite reaches halfway up. This is because when
Sin(0.02 * T) reaches its minimum -1, the -1 goes into the Cos as a radian...
which is a positive value. So, the smile will only go up a radian on each side.
If you want a semicircle-shaped smile, AngFreq will have to be set to Pi / 2 (corresponds
to 90 degrees), so that the circle goes up 90 degrees on each side, forming the
semicircle. Setting AngFreq to Pi or greater will give you a full circle. Greater
values cause the smile to swing back upon itself. Changing an internal Sine to a Cosine
turns the smile into a frown.
The periodics get stranger with our functions as well:
X = 80 + 40 * Hxgn(1.5 * Trpz(0.02 * T))
Y = 120 + 40 * Hxgn(1.5 * Trgl(0.02 * T) + 1)
The red circle does not have the same radius as the white circle in the picture or
in the following pictures.
You can see that this function never quite reaches halfway up. This is because when
Sin(0.02 * T) reaches its minimum -1, the -1 goes into the Cos as a radian...
which is a positive value. So, the smile will only go up a radian on each side.
If you want a semicircle-shaped smile, AngFreq will have to be set to Pi / 2 (corresponds
to 90 degrees), so that the circle goes up 90 degrees on each side, forming the
semicircle. Setting AngFreq to Pi or greater will give you a full circle. Greater
values cause the smile to swing back upon itself. Changing an internal Sine to a Cosine
turns the smile into a frown.
The periodics get stranger with our functions as well:
X = 80 + 40 * Hxgn(1.5 * Trpz(0.02 * T))
Y = 120 + 40 * Hxgn(1.5 * Trgl(0.02 * T) + 1)
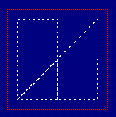 Modifying the offset gives us different results as well. Some of these results can only
be fully appreciated by watching the designs draw themselves live. Others, of course,
draw themselves out nicely.
Origin + Radius * F1(AngFreq1 * T + offset1 + F2(AngFreq2 * T + offset2))
X = 80 + 40 * Sin(0.05 * T + Sin(0.05 * T))
Y = 120 + 40 * Cos(0.05 * T + Cos(0.05 * T))
Modifying the offset gives us different results as well. Some of these results can only
be fully appreciated by watching the designs draw themselves live. Others, of course,
draw themselves out nicely.
Origin + Radius * F1(AngFreq1 * T + offset1 + F2(AngFreq2 * T + offset2))
X = 80 + 40 * Sin(0.05 * T + Sin(0.05 * T))
Y = 120 + 40 * Cos(0.05 * T + Cos(0.05 * T))
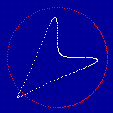 Despite the seemingly insignificant offset functions, the graph looks
nothing like a circle, because when Sin(0.05 * T) reaches its maximum at 1,
Sin(0.05 * T + 1) is not at the maximum, since it is offset by a
radian at this point. However, when Sin(0.05 * T) reaches its maximum,
Cos(0.05 * T) reaches 0, which also causes Cos(0.05 * T + Cos(0.05 * T))
to reach 0. This point corresponds with none of the four endpoints of the
arrowhead, but is a point in the middle of the horizontal point of the
arrowhead.
There are lots more functions out there, some named after other people and some that have no name.
Good luck.
Despite the seemingly insignificant offset functions, the graph looks
nothing like a circle, because when Sin(0.05 * T) reaches its maximum at 1,
Sin(0.05 * T + 1) is not at the maximum, since it is offset by a
radian at this point. However, when Sin(0.05 * T) reaches its maximum,
Cos(0.05 * T) reaches 0, which also causes Cos(0.05 * T + Cos(0.05 * T))
to reach 0. This point corresponds with none of the four endpoints of the
arrowhead, but is a point in the middle of the horizontal point of the
arrowhead.
There are lots more functions out there, some named after other people and some that have no name.
Good luck.
 The red shows the circle without the 10 * Sin(0.4 * T)
The white shows the circle with the sine function added to it. As you
may be able to tell, the radius of this new figure is about 50
in the vertical direction.
Also, we can do
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.4 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.4 * T)
to get
The red shows the circle without the 10 * Sin(0.4 * T)
The white shows the circle with the sine function added to it. As you
may be able to tell, the radius of this new figure is about 50
in the vertical direction.
Also, we can do
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.4 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.4 * T)
to get
 You may wonder why there are 7 loops? It does not have anything to do
with the 50 and 120 being 70 apart. The seven loops come from the
two different angular frequencies... the second angular frequency is
8 times the first angular frequency. That might not appear to explain the
seven loops, but it does if you consider the entire circle to be a loop as
well. After all, if you set the second frequency to be the same as the
first, then you get a plain circle (you can see by doing some algebra)
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.05 * T)
is equivalent to
X = 50 + 50 * Cos(0.05 * T)
Y = 120 + 50 * Sin(0.05 * T)
So, that would be one loop, and
You may wonder why there are 7 loops? It does not have anything to do
with the 50 and 120 being 70 apart. The seven loops come from the
two different angular frequencies... the second angular frequency is
8 times the first angular frequency. That might not appear to explain the
seven loops, but it does if you consider the entire circle to be a loop as
well. After all, if you set the second frequency to be the same as the
first, then you get a plain circle (you can see by doing some algebra)
X = 50 + 40 * Cos(0.05 * T) + 10 * Cos(0.05 * T)
Y = 120 + 40 * Sin(0.05 * T) + 10 * Sin(0.05 * T)
is equivalent to
X = 50 + 50 * Cos(0.05 * T)
Y = 120 + 50 * Sin(0.05 * T)
So, that would be one loop, and
 has eight loops: seven on the inside, surrounded by one big loop.
We can add any kind of periodic functions together. The only
constraint that we have with doing periodics is that all of the
function calls with T have to be periodic. So, we can have
something like this
X = 50 + 20 * Cos(0.01 * T) + 10 * Cos(0.07 * T) + 20 * Hxgn(0.02 * T)
Y = 120 + 40 * Sin(0.01 * T) + 10 * Sin(0.07 * T) + 10 * Trpz(0.002 * T)
Of course it looks like scribble scratch because the periods of
Hxgn and Trpz don't match Sine and Cosine's period... eww.
has eight loops: seven on the inside, surrounded by one big loop.
We can add any kind of periodic functions together. The only
constraint that we have with doing periodics is that all of the
function calls with T have to be periodic. So, we can have
something like this
X = 50 + 20 * Cos(0.01 * T) + 10 * Cos(0.07 * T) + 20 * Hxgn(0.02 * T)
Y = 120 + 40 * Sin(0.01 * T) + 10 * Sin(0.07 * T) + 10 * Trpz(0.002 * T)
Of course it looks like scribble scratch because the periods of
Hxgn and Trpz don't match Sine and Cosine's period... eww.
 A nicer pic can be made by taking functions with similar periods and using
angular frequencies that have common factors.
For example:
X = 80 + 40 * Hxgn(0.01 * T) + 10 * Scln(0.05 * T) + 10 * Trpz(0.05 * T)
Y = 120 + 40 * Hxgn(0.01 * T + 1) + 15 * Scln(0.05 * T + 1)
A nicer pic can be made by taking functions with similar periods and using
angular frequencies that have common factors.
For example:
X = 80 + 40 * Hxgn(0.01 * T) + 10 * Scln(0.05 * T) + 10 * Trpz(0.05 * T)
Y = 120 + 40 * Hxgn(0.01 * T + 1) + 15 * Scln(0.05 * T + 1)
 It looks a little horrendous at the start, but you can see that it
comes to a nice closure within three loops.
Note that in addition to addition (oops, no pun intended), we can combine
two periodic functions with multiplication.
(The radius changes according to a periodic function)
We'll have something like
Origin + Radius1 * Radius2 * F1(AngFreq * T + offset) * F2(AngFreq * T + offset)
The product of the two periodic functions will also be periodic, going
from -1 to 1.
So, we can have something like this:
X = 80 + 40 * Sin(0.02 * T) * Cos(0.06 * T)
Y = 120 + 40 * Cos(0.02 * T) * Cos(0.06 * T)
It looks a little horrendous at the start, but you can see that it
comes to a nice closure within three loops.
Note that in addition to addition (oops, no pun intended), we can combine
two periodic functions with multiplication.
(The radius changes according to a periodic function)
We'll have something like
Origin + Radius1 * Radius2 * F1(AngFreq * T + offset) * F2(AngFreq * T + offset)
The product of the two periodic functions will also be periodic, going
from -1 to 1.
So, we can have something like this:
X = 80 + 40 * Sin(0.02 * T) * Cos(0.06 * T)
Y = 120 + 40 * Cos(0.02 * T) * Cos(0.06 * T)
 You can clearly see the 3 prongs of the fan are due to 0.06 being 3 times 0.02.
What you may not see is that changing the second pair of angular frequencies to
8 gives you eight fan blades, instead of 4 that you might expect.
This is because at the halfway point, Cos(0.02 * T) is halfway finished with the
circle and is -1, Cos(0.06 * T) is also halfway at -1. These two -1s multiply
together to give a +1, which means that at the halfway point, the periodic function
completes a lap. At the halfway point of Cos(0.02 * T), Cos(0.08 * T) has
already returned to the beginning, so it is at 1, and these multiply together to
give -1, so the drawing has not completed yet.
Of course, you can multiply more together to get something like
You can clearly see the 3 prongs of the fan are due to 0.06 being 3 times 0.02.
What you may not see is that changing the second pair of angular frequencies to
8 gives you eight fan blades, instead of 4 that you might expect.
This is because at the halfway point, Cos(0.02 * T) is halfway finished with the
circle and is -1, Cos(0.06 * T) is also halfway at -1. These two -1s multiply
together to give a +1, which means that at the halfway point, the periodic function
completes a lap. At the halfway point of Cos(0.02 * T), Cos(0.08 * T) has
already returned to the beginning, so it is at 1, and these multiply together to
give -1, so the drawing has not completed yet.
Of course, you can multiply more together to get something like
 fX = 80 + 40 * Sin(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
fY = 120 + 40 * Cos(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
Where the six big prongs come from the 0.06 and the 0.02, and the four smaller
prongs combining to make 10 prongs in total come from 0.1 and 0.02.
Remember that the only constraint is that T must be in a periodic function.
So, we have had periodic addition where "the origin change by a periodic function", and
we had periodic multiplication where "the radius changes by a periodic function".
Of course, we can make the final two parameters change by periodic functions... namely the
angular frequency and the offset.
With the angular frequency modified, we'll have something like this:
Origin + Radius * F1(AngFreq1 * F2(AngFreq2 * T + offset2) + offset1)
(The radius and angfreq multiplied to give the AngFreq1.
AngFreq1 has to be suitably large, otherwise the function might appear to be stuck
at a certain value.
X = 80 + 40 * Sin(1 * Sin(0.02 * T))
Y = 120 + 40 * Cos(1 * Sin(0.02 * T))
fX = 80 + 40 * Sin(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
fY = 120 + 40 * Cos(0.02 * T) * Sin(0.06 * T) * Sin(0.1 * T)
Where the six big prongs come from the 0.06 and the 0.02, and the four smaller
prongs combining to make 10 prongs in total come from 0.1 and 0.02.
Remember that the only constraint is that T must be in a periodic function.
So, we have had periodic addition where "the origin change by a periodic function", and
we had periodic multiplication where "the radius changes by a periodic function".
Of course, we can make the final two parameters change by periodic functions... namely the
angular frequency and the offset.
With the angular frequency modified, we'll have something like this:
Origin + Radius * F1(AngFreq1 * F2(AngFreq2 * T + offset2) + offset1)
(The radius and angfreq multiplied to give the AngFreq1.
AngFreq1 has to be suitably large, otherwise the function might appear to be stuck
at a certain value.
X = 80 + 40 * Sin(1 * Sin(0.02 * T))
Y = 120 + 40 * Cos(1 * Sin(0.02 * T))
 The red circle does not have the same radius as the white circle in the picture or
in the following pictures.
You can see that this function never quite reaches halfway up. This is because when
Sin(0.02 * T) reaches its minimum -1, the -1 goes into the Cos as a radian...
which is a positive value. So, the smile will only go up a radian on each side.
If you want a semicircle-shaped smile, AngFreq will have to be set to Pi / 2 (corresponds
to 90 degrees), so that the circle goes up 90 degrees on each side, forming the
semicircle. Setting AngFreq to Pi or greater will give you a full circle. Greater
values cause the smile to swing back upon itself. Changing an internal Sine to a Cosine
turns the smile into a frown.
The periodics get stranger with our functions as well:
X = 80 + 40 * Hxgn(1.5 * Trpz(0.02 * T))
Y = 120 + 40 * Hxgn(1.5 * Trgl(0.02 * T) + 1)
The red circle does not have the same radius as the white circle in the picture or
in the following pictures.
You can see that this function never quite reaches halfway up. This is because when
Sin(0.02 * T) reaches its minimum -1, the -1 goes into the Cos as a radian...
which is a positive value. So, the smile will only go up a radian on each side.
If you want a semicircle-shaped smile, AngFreq will have to be set to Pi / 2 (corresponds
to 90 degrees), so that the circle goes up 90 degrees on each side, forming the
semicircle. Setting AngFreq to Pi or greater will give you a full circle. Greater
values cause the smile to swing back upon itself. Changing an internal Sine to a Cosine
turns the smile into a frown.
The periodics get stranger with our functions as well:
X = 80 + 40 * Hxgn(1.5 * Trpz(0.02 * T))
Y = 120 + 40 * Hxgn(1.5 * Trgl(0.02 * T) + 1)
 Modifying the offset gives us different results as well. Some of these results can only
be fully appreciated by watching the designs draw themselves live. Others, of course,
draw themselves out nicely.
Origin + Radius * F1(AngFreq1 * T + offset1 + F2(AngFreq2 * T + offset2))
X = 80 + 40 * Sin(0.05 * T + Sin(0.05 * T))
Y = 120 + 40 * Cos(0.05 * T + Cos(0.05 * T))
Modifying the offset gives us different results as well. Some of these results can only
be fully appreciated by watching the designs draw themselves live. Others, of course,
draw themselves out nicely.
Origin + Radius * F1(AngFreq1 * T + offset1 + F2(AngFreq2 * T + offset2))
X = 80 + 40 * Sin(0.05 * T + Sin(0.05 * T))
Y = 120 + 40 * Cos(0.05 * T + Cos(0.05 * T))
 Despite the seemingly insignificant offset functions, the graph looks
nothing like a circle, because when Sin(0.05 * T) reaches its maximum at 1,
Sin(0.05 * T + 1) is not at the maximum, since it is offset by a
radian at this point. However, when Sin(0.05 * T) reaches its maximum,
Cos(0.05 * T) reaches 0, which also causes Cos(0.05 * T + Cos(0.05 * T))
to reach 0. This point corresponds with none of the four endpoints of the
arrowhead, but is a point in the middle of the horizontal point of the
arrowhead.
There are lots more functions out there, some named after other people and some that have no name.
Good luck.
Despite the seemingly insignificant offset functions, the graph looks
nothing like a circle, because when Sin(0.05 * T) reaches its maximum at 1,
Sin(0.05 * T + 1) is not at the maximum, since it is offset by a
radian at this point. However, when Sin(0.05 * T) reaches its maximum,
Cos(0.05 * T) reaches 0, which also causes Cos(0.05 * T + Cos(0.05 * T))
to reach 0. This point corresponds with none of the four endpoints of the
arrowhead, but is a point in the middle of the horizontal point of the
arrowhead.
There are lots more functions out there, some named after other people and some that have no name.
Good luck.