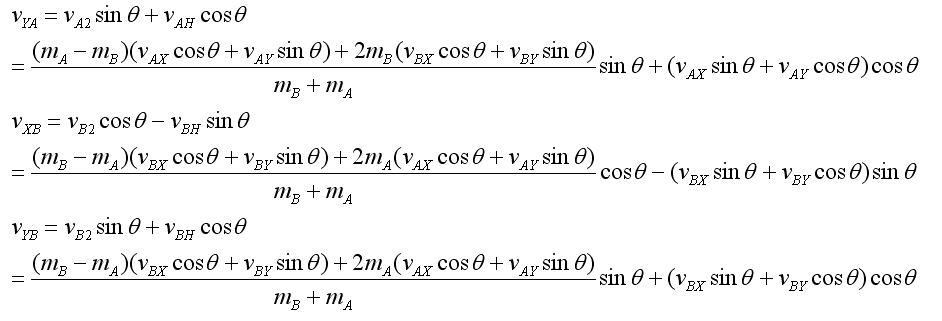



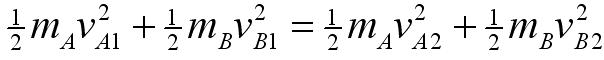
 can be shuffled around for similar masses on one side
can be shuffled around for similar masses on one side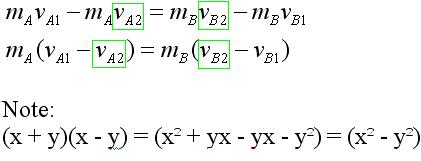



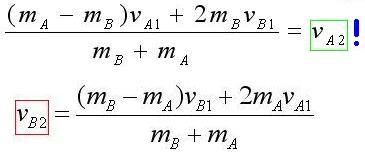

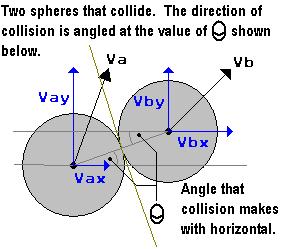


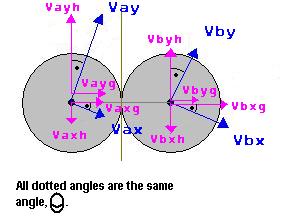
| Vaxg = Vax * Cos(Angle) | Vaxh = Vax * Sin(Angle) | Vayg = Vay * Sin(Angle) | Vayh = Vay * Cos(Angle) |
| Vbxg = Vbx * Cos(Angle) | Vbxh = Vbx * Sin(Angle) | Vbyg = Vby * Sin(Angle) | Vbyh = Vby * Cos(Angle) |

| Vag = Vaxg + Vayg = Vax * Cos(Angle) + Vay * Sin(Angle) | Vah = Vaxh + Vayh = Vax * Sin(Angle) + Vayh = Vay * Cos(Angle) |
| Vbg = Vbxg + Vbyg = Vbx * Cos(Angle) + Vby * Sin(Angle) | Vbh = Vbxh + Vbyh = Vbx * Sin(Angle) + Vbyh = Vby * Cos(Angle) |
 .
.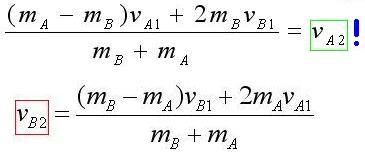
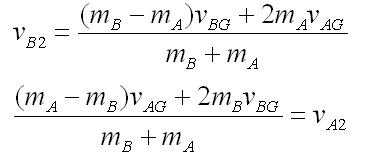
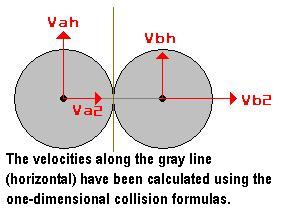

| Va2x = Va2 * Cos(Angle) | Va2y = Va2 * Sin(Angle) | Vahx = Vah * Sin(Angle) | Vahy = Vah * Cos(Angle) |
| Vb2x = Vb2 * Cos(Angle) | Vb2y = Vb2 * Sin(Angle) | Vbhx = Vbh * Sin(Angle) | Vbhy = Vbh * Cos(Angle) |

| Vxa = Va2x - Vahx = Va2 * Cos(Angle) - Vah * Sin(Angle) | Vya = Va2y + Vahy = Va2 * Sin(Angle) + Vah * Cos(Angle) |
| Vxb = Vb2x - Vbhx = Vb2 * Cos(Angle) - Vbh * Sin(Angle) | Vyb = Vb2y + Vbhy = Vb2 * Sin(Angle) + Vbh * Cos(Angle) |